[자료구조] 트리 - Trees(Part 1)

2023-05-02 7 분 소요

트리 - Trees

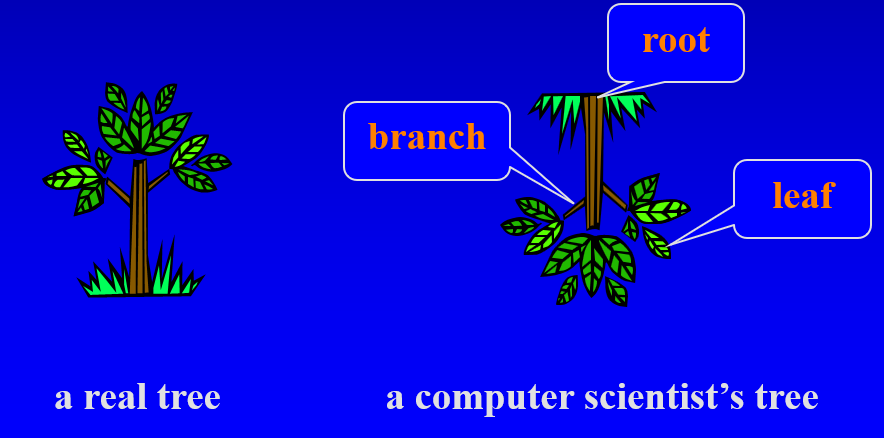
트리란?

트리는 비선형 구조다.
즉, 구성요소는 첫번째 엔트리, 두 번째 엔트리, 세 번째 엔트리등의 단순한 시퀀스를 형성하지 않는다.
체인처럼 연결된 구조가아닌 가지가 뻗어나가는 구조다.
트리에는 비어 있을 수 있는 한정된 노드 집합이 있다.
한 종류 또는 다른 종류의 데이터는 각 노드에 저장될 수 있다.

Definitions

Node	Definitions
Parent - 부모	노드 위에 연결된 노드
Child(ren) - 자식	노드 아래에 연결된 노드
Siblings - 형제	부모가 같은 노드
Root(of a tree)	부모가 없는 특수 노드
Leaf	자식이 없는 노드
Ancestor (of a node)	노드의 부모는 조상, 부모의 모든 조상은 조상
Descendant (of a node)	노드의 자식은 그 자손, 자녀의 모든 후손은 그 후손
Subtree (of a tree)	원래 트리 내의 더 작은 트리
Depth of a node(노드의 깊이)	노드에서 루트까지의 단계 수
Depth of a tree(트리의 깊이)	leaves의 가장 큰 깊이

Binary Trees

바이너리 트리

각 노드는 최대 두 개의 자식(왼쪽 자식과 오른쪽 자식)을 가질 수 있음
노드의 왼쪽 아래 트리는 루트가 왼쪽 자식인 하위 트리
노드의 오른쪽 아래 트리는 루트가 오른쪽 자식인 하위 트리

Full Binary Trees는 모든 리프가 동일한 깊이이며 리프가 아닌 노드는 두개의 자식이 있는 트리다.

Complete Binary Trees는 가장 깊은 레벨에는 가능한 많은 노드가 포함되어야 하고 모든 노드는 가능한 한 멀리 왼쪽에 있어야 한다.

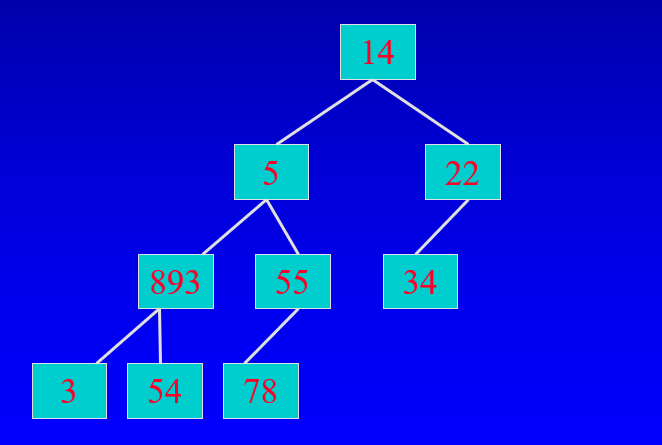
Ex. 다음은 complete 인가? -> no

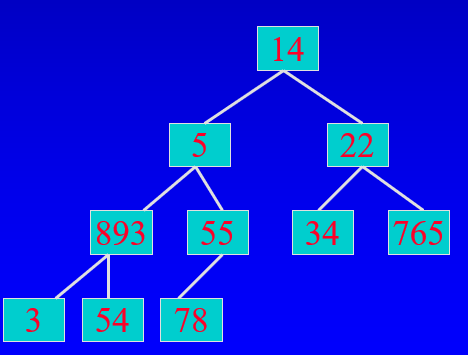
Ex. 다음은 complete 인가? -> yes

Tree Representations

트리를 표현하는 방법

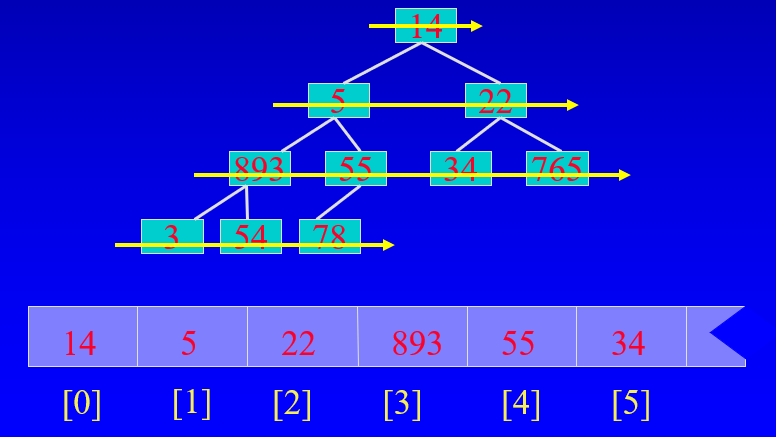
1.이진 트리의 배열 표현을 한다.

자세히 살펴보면 트리의 수식을 확인할 수 있다.

left child : [2i + 1]
left child : [2i + 2]

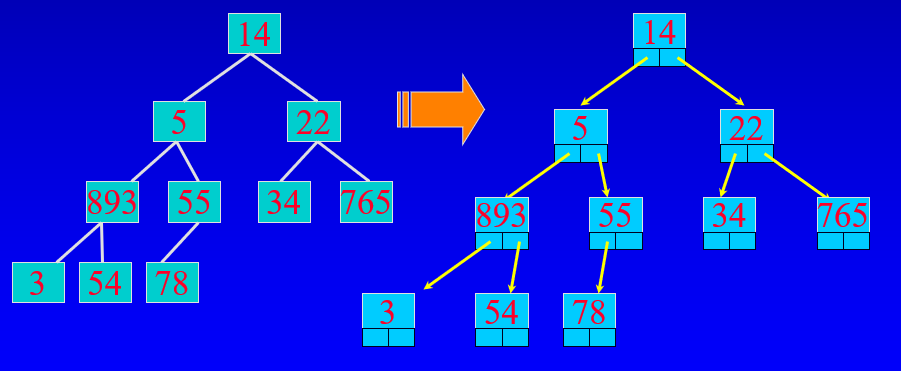
2.노드 클래스로 이진 트리를 표현한다.

다음은 3가지 멤버 변수를 갖는다.

data_field : 데이터 저장을 위해
left_field : 왼쪽 자식 노드에 대한 포인터
right field : 오른쪽 자식에 대한 포인터

바이너리 트리 노드

클래스 구현

constructor

binary_tree_node(
	const Item& init_data = Item(),
	binary_tree_node* init_left = NULL,
  binary_tree_node* init_right = NULL)
{    
	data_field  = init_data ;
	left_field = init_left ;
	right_field = init_right ;
} 

data

Item& data( ) //&는 n->data=42;라는 표현도 가능하다.
// 보통은 Item a = n.data();
{    
  return data_field ;
} 

left

binary_tree_node*&  left( )
{    
	return left_field ;
}

right

binary_tree_node*& right( )
{    
	return right_field ;
} 

set_data(…)

void set_data(const item& new_data) { data_field = new_data ;}

set_left(…)

void set_left(binary_tree_node* new_left) { left_field = new_left ; } 

set_right(…)

void set_right(binary_tree_node* new_right) { right_field = new_right ; } 

is_leaf()

bool is_leaf( ) const 
{
	return (left_field == NULL &&
					right_field == NULL) ;
}

함수 구현

tree_clear

template <class Item>
void tree_clear(binary_tree_node<Item>*& root_ptr)
{
	if(root_ptr != NULL)
	{
		tree_clear(root_ptr -> left());
		tree_clear(root_ptr -> right());
		delete root_ptr;
		root_ptr = NULL;
	}
} 

tree_copy

binary_tree_node<Item>* tree_copy(binary_tree_node<Item>* root_ptr){
	binary_tree_node<Item> *l_ptr;
	binary_tree_node<Item> *r_ptr;

	if(root_ptr == NULL)
		return NULL;
	else{
		l_ptr = tree_copy(root_ptr -> left());
		r_ptr = tree_copy(root_ptr -> right());
		return new binary_tree_node<Item>(root_ptr -> data(), l_ptr, r_ptr);
	}
}

Tree Traversals

이진 트리의 Traversals

트리 트레버셜은 각 노드에 일부 작업을 적용해 트리의 모든 노드를 처리한다.

Ex. 트리의 모든 데이터 값 프린팅, 트리의 모든 데이터 값 업데이트
일반적인 트레버셜 방법 3가지가 있는데 이는 루트가 처리되는 시기에 따라 나뉜다.
pre-order, in-order, post-order

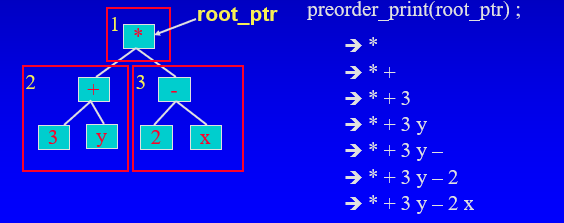
pre-order

먼저 루트를 처리한다.
리커시브 호출을 사용해 왼쪽 서브트리의 노드를 처리한다.
리커시브 호춯을 사용해 오른쪽 서브트리의 노드를 처리한다.

template <class Item>
void preorder_print(const binary_tree_node<Item>* root_ptr)
{
	if (root_ptr != NULL)
  	{
			cout << root_ptr->data( ) << endl;
			// root_ptr의 데이터를 먼저 출력
      preorder_print( root_ptr->left( ) ) ;
      preorder_print( root_ptr->right( ) ) ;
    }
}

실행결과

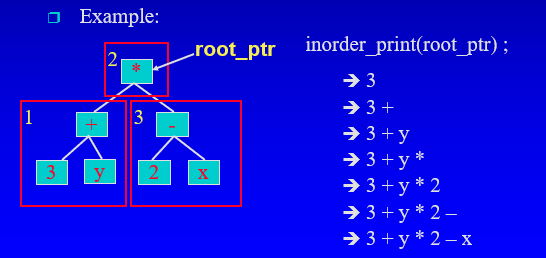
in-order

리커시브 호출을 사용해 왼쪽 서브트리의 노드를 처리한다.
루트를 처리한다.
리커시브 호출을 사용해 오른쪽 서브트리의 노드를 처리한다.

template <class Item>
void inorder_print(const binary_tree_node<Item>* root_ptr)
{
	if (root_ptr != NULL)
		{
			inorder_print( root_ptr->left( ) ) ;
      cout << root_ptr->data( ) << endl;
      inorder_print( root_ptr->right( ) ) ;
    }
}

실행결과

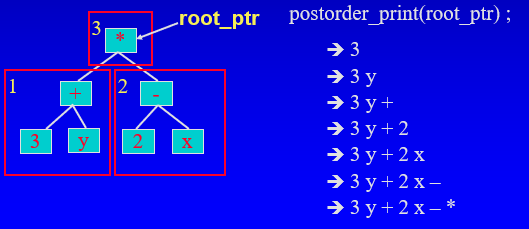
post-order

리커시브 호출을 사용해 왼쪽 서브트리의 노드를 처리한다.
리커시브 호출을 사용해 오른쪽 서브트리의 노드를 처리한다.
마지막으로 루트를 처리한다.

template <class Item>
void postorder_print(const binary_tree_node<Item>* root_ptr)
{
  if (root_ptr != NULL)
    {
    	postorder_print( root_ptr->left( ) ) ;
    	postorder_print( root_ptr->right( ) ) ;
      cout << root_ptr->data( ) << endl;
    }
} 

실행결과

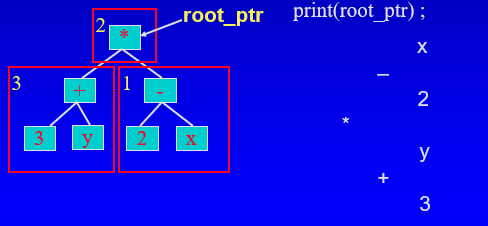
Backward in-order

트리형태(90도 회전)와 같은 노드를 빠르게 프린트하는데 유용하다.
아래 실습코드는 시각적으로 트리를 90도 회전시켜 프린트해보겠다.

리커시브 호출을 사용해 오른쪽 서브트리의 노드를 처리한다.
루트를 처리한다.
리커시브 호출을 사용해 왼쪽 서브트리의 노드를 처리한다.

template <class Item, class SizeType>
void print(const binary_tree_node<Item>* root_ptr, SizeType depth)
{
  if (root_ptr != NULL)
  	{
    	print( root_ptr->right( ), depth+1 ) ;
      cout << setw(4*depth) << “” << root_ptr->data( )<< endl;
			//setw : 는 space를 나타냄(#include <iomanip>)
	    print( root_ptr->left( ), depth+1 ) ;
    }
}

실행결과

트레버셜의 문제점

100가지 다른 종류의 처리를 수행한다고 가정해보자
Ex. 프린팅, 데이터 1씩증가, 각 데이터 값에 -1곱하기등등,,,
100가지의 함수 및 기능들이 필요하다.
따라서 함수 매개변수를 사용한다!!!
함수 자체를 파라미터로 사용해야한다.

파라미터 함수

Ex. 다음과 같이 함수가 파라미터로 사용되는 예시

void apply(void f(int&), int data[ ], size_t n)
{ 
	size_t	i;
	for(i=0; i<n ; i++)
		f(data[i]);
}
void add1(int& i)  {i += 1;}
void triple(int& i)  {i *= 3;}

실행결과

Ex. 템플릿 버전으로 수정한 버전(범용성이 넓어짐)

template <class Item, class SizeType>
void apply(void f(Item&), Item data[ ], SizeType n)
// 아직 보이드여야만 한다
{ 
	SizeType	i;
	for (i=0; i<n ; i++)
		f(data[i]);
}
void add1(int& i){i += 1;}
void toUpperCase(char& c){c = toupper(c);} // cctype

Ex. 템플릿 버전을 더 범용성있게 만든 버전

template <class Process, class Item, class SizeType>
void apply(Process f, Item data[ ], SizeType n)
{ 
	SizeType   i ;
	for (i=0; i<n ; i++)
		f(data[i]) ;
		// f는 단일 항목 아규먼트로 호출할 수 있습니다.
}
void add1(int& i)  {i += 1;}
void print(double d)  {cout << d << endl;} 

트리 트레버셜을 위한 템플릿 기능

위에서 알아봤드시 파라미터가 함수일 수 있다.
일부 컴파일러는 함수 자체인 매걔변수가 있는 템플릿 함수의 사용을 지원하지 않을 수 있다.(devc++, vscord는 가능)

template <class Process, class BTNode>
void preorder(Process f, BTNode* node_ptr)
{ 
	if (node_ptr != NULL)
	{
		f( node_ptr->data( ));
		preorder(f, node_ptr->left( ));
		preorder(f, node_ptr->right( ));
	}
}

배운 내용들 실습

bintree.template 파일

// FILE: bintree.template
#include <cassert>    // Provides assert
#include <cstdlib>   // Provides NULL, std::size_t
#include <iomanip>    // Provides std::setw
#include <iostream>   // Provides std::cout

namespace main_savitch_10
{
    template <class Process, class BTNode>
    void inorder(Process f, BTNode* node_ptr)
    // Library facilities used: cstdlib
    {
        if (node_ptr != NULL)
        {
            inorder(f, node_ptr->left( ));
            f( node_ptr->data( ) );
            inorder(f, node_ptr->right( ));
        }
    }

    template <class Process, class BTNode>
    void postorder(Process f, BTNode* node_ptr)
    // Library facilities used: cstdlib
    {
        if (node_ptr != NULL)
        {
            postorder(f, node_ptr->left( ));
            postorder(f, node_ptr->right( ));
            f(node_ptr->data( ));
        }
    }

    template <class Process, class BTNode>
    void preorder(Process f, BTNode* node_ptr)
    // Library facilities used: cstdlib
    {
        if (node_ptr != NULL)
        {
            f( node_ptr->data( ) );
            preorder(f, node_ptr->left( ));
            preorder(f, node_ptr->right( ));
        }
    }

    template <class Item, class SizeType>
    void print(binary_tree_node<Item>* node_ptr, SizeType depth)
    // Library facilities used: iomanip, iostream, stdlib
    {
        if (node_ptr != NULL)
        {
            print(node_ptr->right( ), depth+1);
            std::cout << std::setw(4*depth) << ""; // Indent 4*depth spaces.
            std::cout << node_ptr->data( ) << std::endl;
            print(node_ptr->left( ),  depth+1);
        }
    }    
	
    template <class Item>
    void tree_clear(binary_tree_node<Item>*& root_ptr)
    // Library facilities used: cstdlib
    {
	binary_tree_node<Item>* child;
	if (root_ptr != NULL)
	{
	    child = root_ptr->left( );
	    tree_clear( child );
	    child = root_ptr->right( );
	    tree_clear( child );
	    delete root_ptr;
	    root_ptr = NULL;
	}
    }

    template <class Item>
    binary_tree_node<Item>* tree_copy(const binary_tree_node<Item>* root_ptr)
    // Library facilities used: cstdlib
    {
	binary_tree_node<Item> *l_ptr;
	binary_tree_node<Item> *r_ptr;

	if (root_ptr == NULL)
	    return NULL;
	else
	{
	    l_ptr = tree_copy( root_ptr->left( ) );
	    r_ptr = tree_copy( root_ptr->right( ) );
	    return
		new binary_tree_node<Item>( root_ptr->data( ), l_ptr, r_ptr);
	}
    }

    template <class Item>
    size_t tree_size(const binary_tree_node<Item>* node_ptr)
    // Library facilities used: cstdlib
    {
        if (node_ptr == NULL)
            return 0;
        else 
            return 
	    1 + tree_size(node_ptr->left( )) + tree_size(node_ptr->right( ));
    }    
}

bintree.h파일

// FILE: bintree.h
#ifndef BINTREE_H
#define BINTREE_H
#include <cstdlib>  // Provides NULL and size_t

namespace main_savitch_10
{

	template <class Item>
	class binary_tree_node
	{
	public:
		// TYPEDEF
		typedef Item value_type;
		// CONSTRUCTOR
		binary_tree_node(
			const Item& init_data = Item(),
			binary_tree_node* init_left = NULL,
			binary_tree_node* init_right = NULL
		)
		{
			data_field = init_data;
			left_field = init_left;
			right_field = init_right;
		}
		// MODIFICATION MEMBER FUNCTIONS
		Item& data() { return data_field; }
		binary_tree_node*& left() { return left_field; }
		binary_tree_node*& right() { return right_field; }
		void set_data(const Item& new_data) { data_field = new_data; }
		void set_left(binary_tree_node* new_left) { left_field = new_left; }
		void set_right(binary_tree_node* new_right) { right_field = new_right; }
		// CONST MEMBER FUNCTIONS
		const Item& data() const { return data_field; }
		const binary_tree_node* left() const { return left_field; }
		const binary_tree_node* right() const { return right_field; }
		bool is_leaf() const
		{
			return (left_field == NULL) && (right_field == NULL);
		}
	private:
		Item data_field;
		binary_tree_node* left_field;
		binary_tree_node* right_field;
	};

	// NON-MEMBER FUNCTIONS for the binary_tree_node<Item>:
	template <class Process, class BTNode>
	void inorder(Process f, BTNode* node_ptr);

	template <class Process, class BTNode>
	void preorder(Process f, BTNode* node_ptr);

	template <class Process, class BTNode>
	void postorder(Process f, BTNode* node_ptr);

	template <class Item, class SizeType>
	void print(binary_tree_node<Item>* node_ptr, SizeType depth);

	template <class Item>
	void tree_clear(binary_tree_node<Item>*& root_ptr);

	template <class Item>
	binary_tree_node<Item>* tree_copy(const binary_tree_node<Item>* root_ptr);

	template <class Item>
	std::size_t tree_size(const binary_tree_node<Item>* node_ptr);
}

#include "bintree.template"
#endif

실습내용을 확인하기 위한 main.cpp 파일

// FILE: main.cpp
#include <iostream>  // Provides cin, cout
#include <cstdlib>   // Provides EXIT_SUCCESS
#include "bintree.h"
using namespace std;
using namespace main_savitch_10;

void print_tree(int i)
{
    cout << i << " ";
}

int main()
{
    binary_tree_node<int>* p1 = new binary_tree_node<int>(1, NULL, NULL);
    binary_tree_node<int>* p2 = new binary_tree_node<int>(2, NULL, NULL);
    binary_tree_node<int>* p3 = new binary_tree_node<int>(3, p1, p2);
    binary_tree_node<int>* p4 = new binary_tree_node<int>(4, p3, NULL);
    binary_tree_node<int>* p5 = new binary_tree_node<int>(5, p4, NULL);

    inorder(print_tree, p5); cout << endl;
    preorder(print_tree, p5); cout << endl;
    postorder(print_tree, p5); cout << endl;
    print(p5, 0);

    return EXIT_SUCCESS;
}

실행결과

Twitter Facebook LinkedIn

[자료구조] 트리 - Trees(Part 1)

트리 - Trees

Definitions

Binary Trees

Tree Representations

바이너리 트리 노드

클래스 구현

함수 구현

Tree Traversals

파라미터 함수

배운 내용들 실습

공유하기

댓글남기기

참고

[알고리즘] 입출력과 사칙연산

[파이썬] Data Structures

[파이썬] Replti을 이용해 파이썬 기초 배우기

[자료구조] Graphs