[자료구조] Graphs
Graphs
이번 포스트에서는 가장 일반적으로 사용되는 데이터 구조인 그래프를 소개한다.
Graph Definitions
Graph
그래프는 노드와 노드 사이의 링크로 구성된 비선형 데이터 구조다.
- 트리와 달리 그래프 노드는 어떤 패턴으로도 연결할 수 있다.
- 그래프는 비어 있을 수 있다.
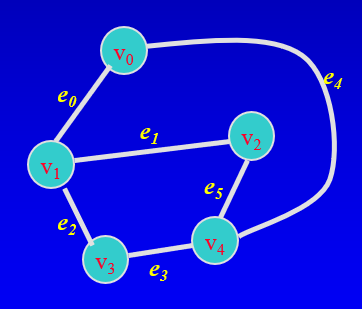
Undirected Graphs
모서리/호(노드 간 링크)의 제한된 세트와 함께 정점(노드)의 제한된 세트
- 가장자리에는 방향이 없다.
- 꼭지점과 가장자리 모두 레이블을 가질 수 있다.
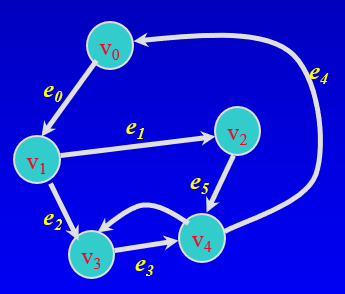
Directed Graphs
제한된 세트의 정점(노드)과 제한된 세트의 방향 모서리/호(노드 간 링크)
- 가장자리에는 방향이 있습니다(소스 -> 타겟).
- 꼭지점과 가장자리 모두 레이블을 가질 수 있다.
More Graph Terminology
추가 그래프 용어
Loop : 본인을 본인에게 연결하는 앳지
Path : 앳지로 연결된 점들의 나열
Cycle : path중 시작점과 끝점이 같은 path
Multiple Edges : 두개의 점사이에 여러개의 앳지가 있는 경우
Simple Graph : 루프와 멀티플 앳지가 없는 그래프
Graph Implementations
Representing Graphs with an Adjacency Matrix
인접 행렬로 그래프 표현하기
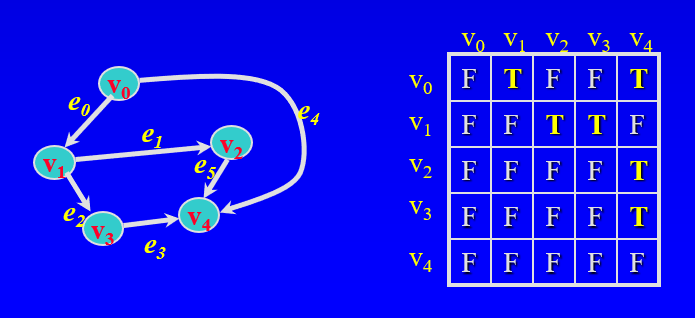
다이렉트 그래프에서의 인접행렬
- 가장자리의 boolean값 또는 엣지의 값의 정사각형 그리드
- Cell[i, j] == true는 점 i에서 j까지 엣지가 있음을 나타냄
- Cell[i, j] == w는 점 i와 j사이 엣지는 w값을 가짐을 나타냄
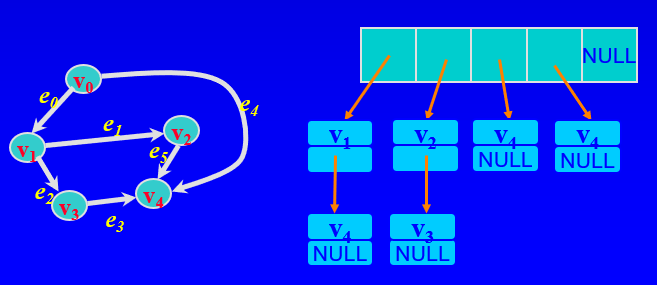
다이렉트 그래프에서의 인접리스트(링크드 리스트)
- n개의 서로 다른 연결 목록의 배열(n = 정점 수)
- 각 배열 셀은 그래프의 점을 나타냄
- 각 배열 셀[i]에는 i에서 직접 연결된 모든 점의 연결 목록에 대한 포인터가 있음
점(vertices)에 값을(weighted) 부여하는 코드 클래스
- private 멤버로 edges값과 labels, vertices의 size를 선언
그래픽 클래스에서의 public 함수들
add_vertex(const Item& label)
add_edge(size_t source, size_t target)
remove_edge(size_t source, size_t target)
operator [ ] (size_t vertex) //
size( )
is_edge(size_t source, size_t target)
set<size_t> neighbors(size_t vertex) const
constructor
- 꼭짓점과 가장자리가 없는 그래프 개체를 만든다.
operator []
- 배열과 같이 적용 점의 index 번호를 받아 labels에 저장
add_vertex
- vertex가 추가되면 기존 0~6 7개에서 size를 index로 추가 7번=new_vertex_number
add_edge
- 소스와 타겟을 받아서 edges[source][target] = true;
is_edge
- 소스와 타겟을 받아서 return edges[source][target];
neighbors
- 버텍스 번호를 받아서 set타입을 answer로 선언해서 for문으로 insert 후 return answer;
remove_edge
- 소스와 타겟을 받아서 edges[source][target] = false;
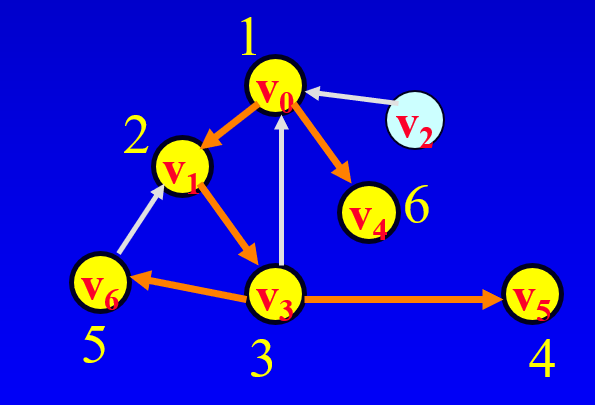
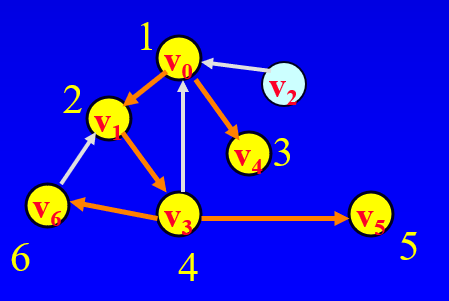
Graph Traversals
그래프 순회
- 그래프에 주기가 있을 수 있으므로 트리 순회와 다르다.
- 반복 방문을 피하기 위해 처리되는 각 vertex를 mark해야함
- 따라서 depth-first search(깊이 우선 검색)과 breadth-first search(폭 우선 탐색)이 있다.
Depth-First Search
깊이 우선 검색
- 검색은 시작 vertex에서 이웃 중 하나로 진행한 다음 이웃의 이웃 중 하나로 진행된다.
- 더 이상 진행할 수 없는 경우 이전 노드로 검색을 백업해야 함
- 스택이나 재귀적으로 구현할 수 있다.
구현
- 재귀적으로 구현한다.
- processFuntion, aGraph, startingVertex를 받는다.
- marked[aGraph.MAX]를 사용해 반복방문을 막는다.
- 1.시작vertex가 유효한 번호인지 확인
- 2.marked[]의 모든 구성요소를 false로 설정
- 별도의 재귀함수(rec_dfs)를 호출해 검색을 수행
Breadth-First Search
폭 우선 검색
- 검색은 시작 정점에서 각 이웃으로 진행
- 모든 이웃을 처리한 후 검색은 이웃의 이웃으로 진행
- 도달 가능한 모든 vertex가 처리되면 검색이 종료
- 큐를 사용해 구현
구현
- 큐로 구현
- processFunction, aGraph, startingVertex을 받음
- marked[aGraph.MAX]를 사용해 반복방문을 막음
- 1_시작 정점이 그래프의 유효한 vertex번호인지 확인
- 2_marked[]를 false로 설정
- 3_시작vertex를 처리하고 marked하고 다음 큐에 넣는다.
- 4_큐가 비워질 때까지 다음단계를 반복
- 4-1_큐에서 vertex, v를 제거
- 4-2_v의 marked되지 않은 각 이웃에 대해 다음을 수행
- 4-2-1_Process u, mark u, and then place u in the queue.
실습
#include <cstdlib> // Provides EXIT_SUCCESS and size_t
#include <iostream> // Provides cin, cout
#include "searches.h"
#include "graph.h"
using namespace std;
using namespace main_savitch_15;
void print_vertex(int i)
{
cout << i << " ";
}
int main()
{
graph<int> g1;
g1.add_vertex(0); g1.add_vertex(1); g1.add_vertex(2); g1.add_vertex(3);
g1.add_vertex(4); g1.add_vertex(5); g1.add_vertex(6); g1.add_vertex(7);
g1.add_edge(0, 1); g1.add_edge(1, 2); g1.add_edge(2, 3); g1.add_edge(3, 7);
g1.add_edge(4, 5); g1.add_edge(5, 6); g1.add_edge(6, 7); g1.add_edge(0, 4);
g1.add_edge(0, 7);
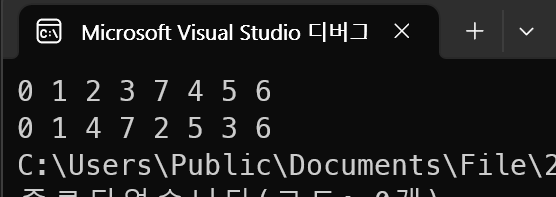
depth_first(print_vertex, g1, 0); cout << endl;
breadth_first(print_vertex, g1, 0);
return EXIT_SUCCESS;
}
댓글남기기